在生物制药生产中制定“控制策略”的重大缺陷

在这篇文章中，我们想指出生物制药生产中设定控制策略（Control strategy）的重大缺陷之一。这与人们仍然根据x-SD方法设定规范（原料药规格或中间体接受标准/过程控制）有关。此外，我们希望展示合理的工具，这些工具能够实现数据驱动设定限值，并在此衍生控制策略（Marschall 等人，2022 年）。

本文主要关注生物制药生产的案例，但可以应用于其他制药和化学工艺，而不会失去通用性。 /p>

了解更多

基于通用数据的方法实现对ICH控制策略的兼容

在典型的工艺开发或工艺表征中，对单个单元操作进行实验，以确定质量合格产品的工艺参数。可以使用诸如统计实验设计（DoE）之类的高效技术来以最少的实验次数达到最大的信息增益。基于工艺输入（如工艺参数和关键材料属性）与输出（通常为关键质量属性（CQA））之间的已确定关系，可以定义输入的控制策略。

典型的数据驱动方法是将模型的不确定性与接受限相交，以得出ICH Q8中所述的已证明的接受范围。

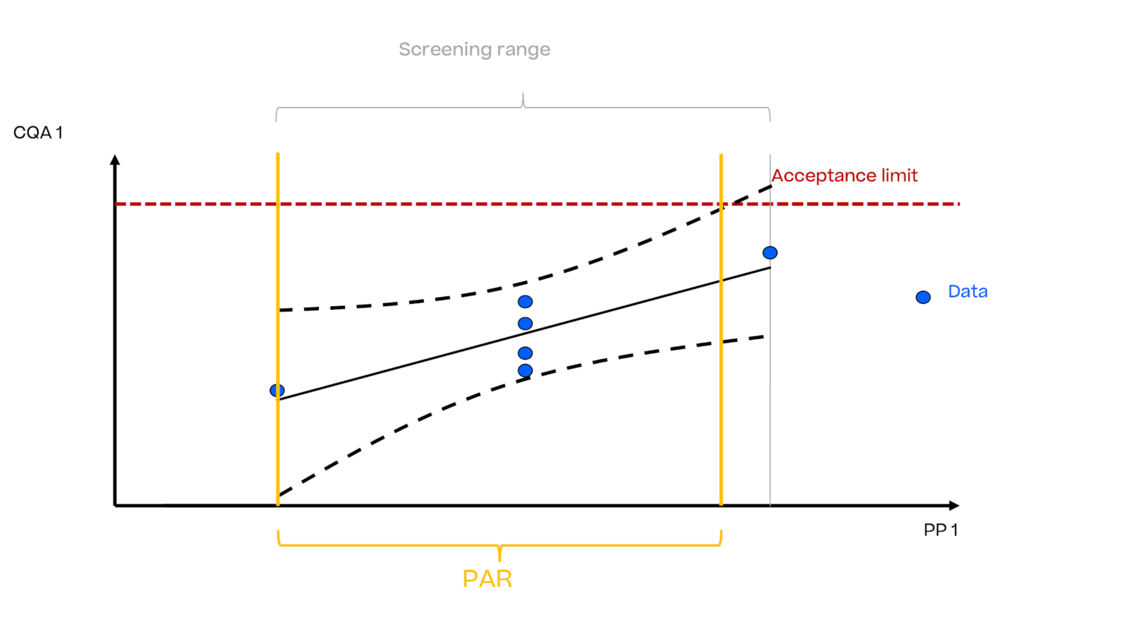
很明显，将接受限作为“把关人”并且明确以下问题：

• 需要计划运行多少次？
• 分析需要有多深入？
• 控制策略的范围需要有多宽？→操作灵活性

需要为每个单元操作和每个CQA建立这些接受限。对于生物制药生产工艺过程，这通常需要10个或更多个单元操作和10个或更多个CQA组成。

为什么设定接受标准的3 SD方法存在缺陷？

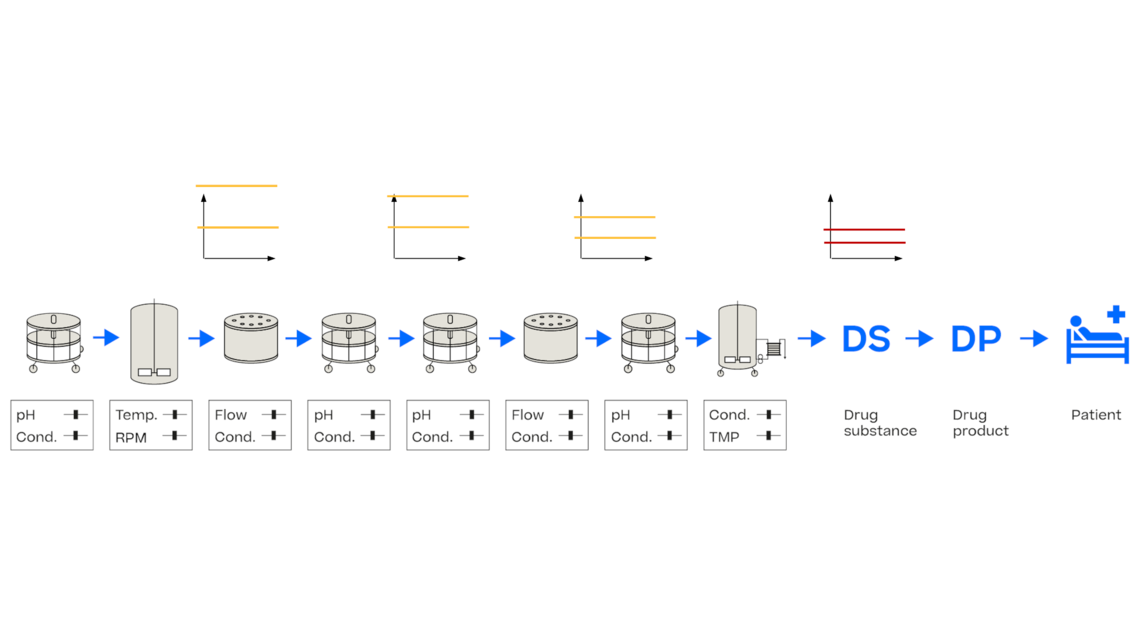
历史上，采用（最常见的是3 SD）的历史生产的平均值的x-SD方法来确定接受限。这些实验通常在生产工艺的设定值（SP）条件下进行。
在工艺开发或工艺表征时，即在工艺生命周期的早期阶段，通常只进行有限次的生产实验，例如3-9次。根据这些实验，可以计算出3 SD，此处描述为误差棒：

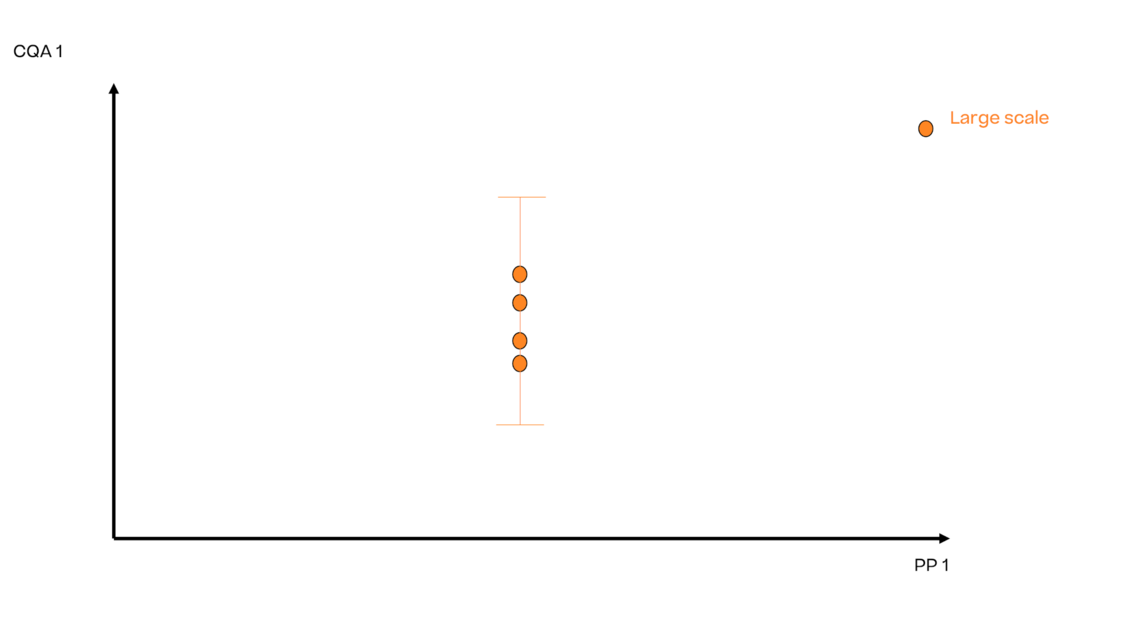
这些限值被视为工艺开发和表征中所有后续工艺的接受标准，通常在小规模下进行。

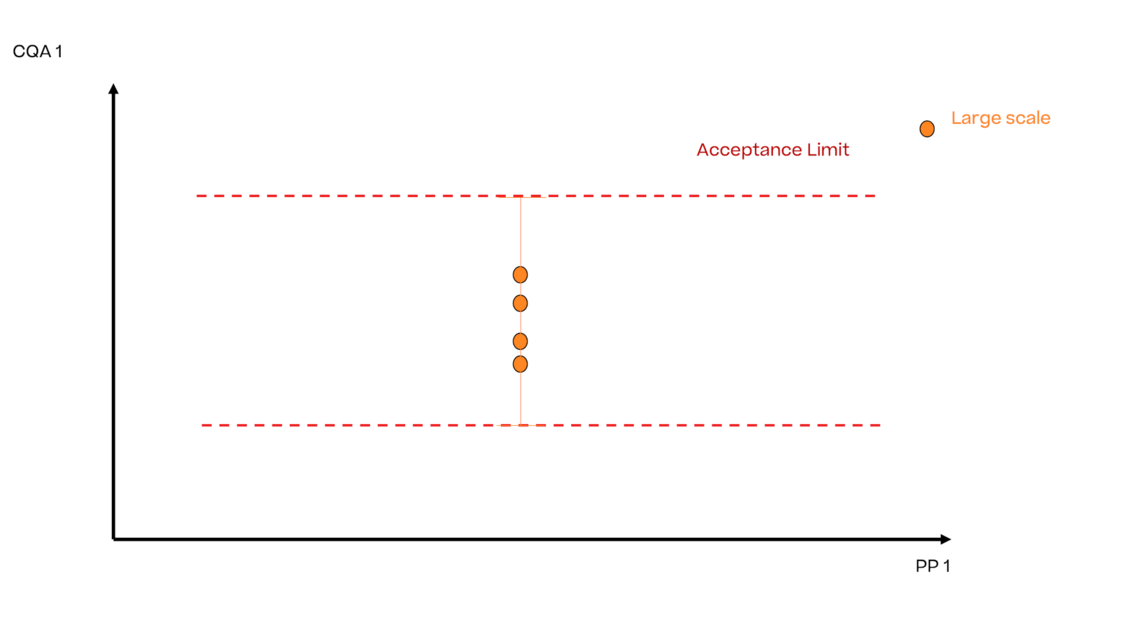
如果小规模数据对大规模数据具有“代表性”（见ICH Q10），则大规模和小规模数据之间不存在偏移且两个方差相同。

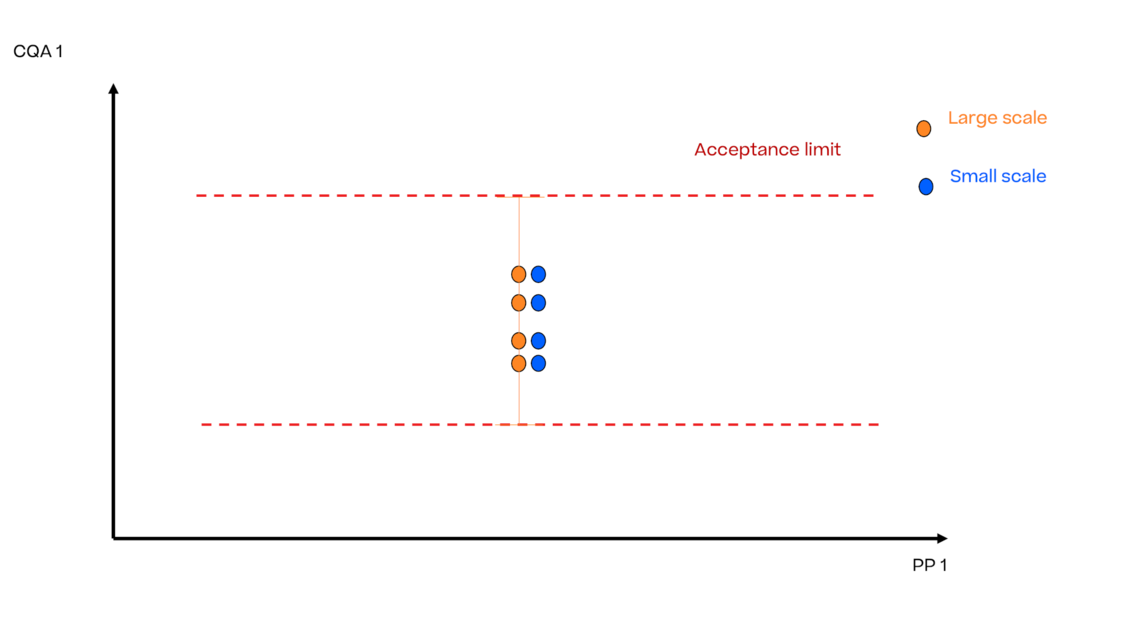
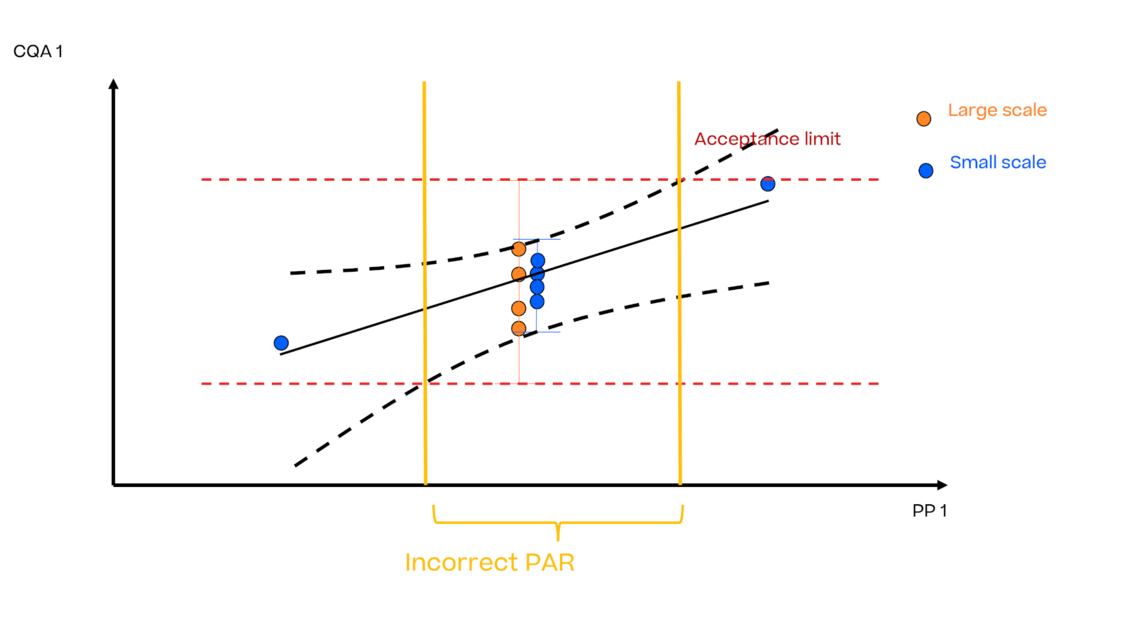
在小范围内有目的地引入工艺参数的偏差，以确定对CQA的平均影响，如实心黑线所示。

为了说明模型的不确定性和残差，我们需要围绕回归平均趋势建立一个不确定性区间。为了不去比较两类完全不同的东西，我们也需要采取xSD--或一些有代表性的公差区间--选择与大规模数据所计算出的可变性的相同的可变性。这些不确定性区间显示为黑色的虚线：

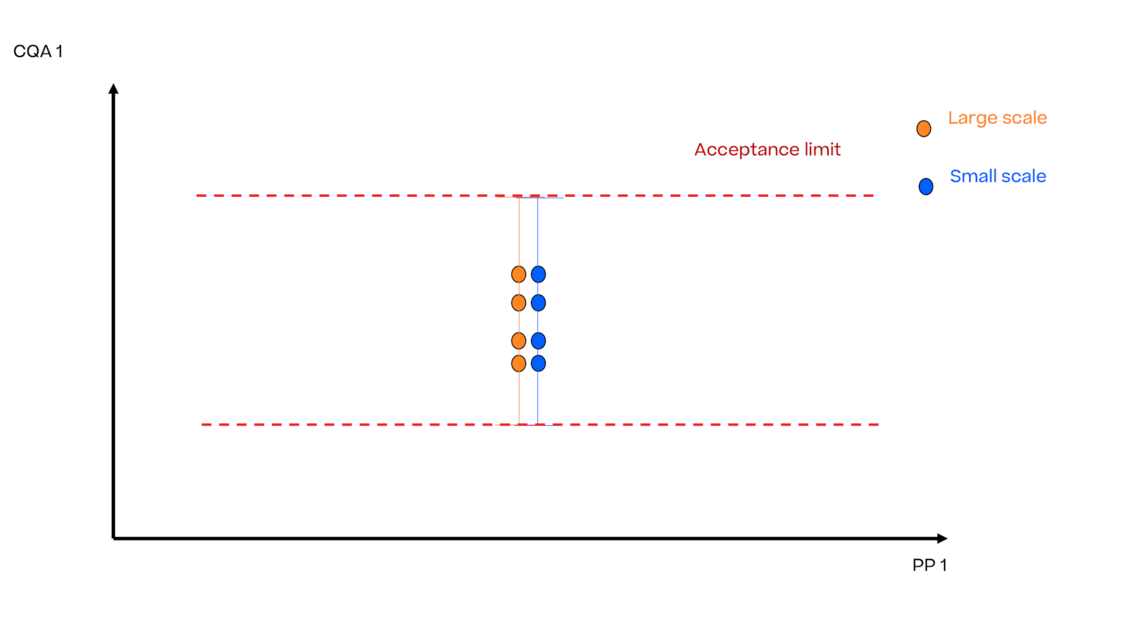
显而易见的是，唯一允许的控制策略是在设定值条件下进行生产，并且不允许任何偏差。

当然，这种控制策略在操作中是不可行的，由于偏离设定值条件的情况经常发生，并会导致大量的偏离数值需要管理。

为什么这种有缺陷仍然出现在文件中？

为什么使用这种方法的静止控制策略仍然成立的两个（有缺陷的）主要原因：

缺陷1

当人们在比较两个不同的东西：例如，模型的不确定性被表示为置信区间（CI），而不是公差区间（TI），然后与3 SD进行比较。置信区间描述的是平均值周围的不确定性，在有大量运行的情况下，它们接近平均值趋势（黑色实线）。很明显，这样的置信区间总是会导致宽泛的控制策略，在统计上是不正确的。尽管它们的名字存在误导性，但预测区间也是如此，它只包涵下一个未来观测数据的不确定性。与此相反，我们希望对未来生产工艺的总体情况进行说明，即证明未来生产的大部分结果是符合规范的。因此，只有公差区间（TI）在统计学上是合适的。

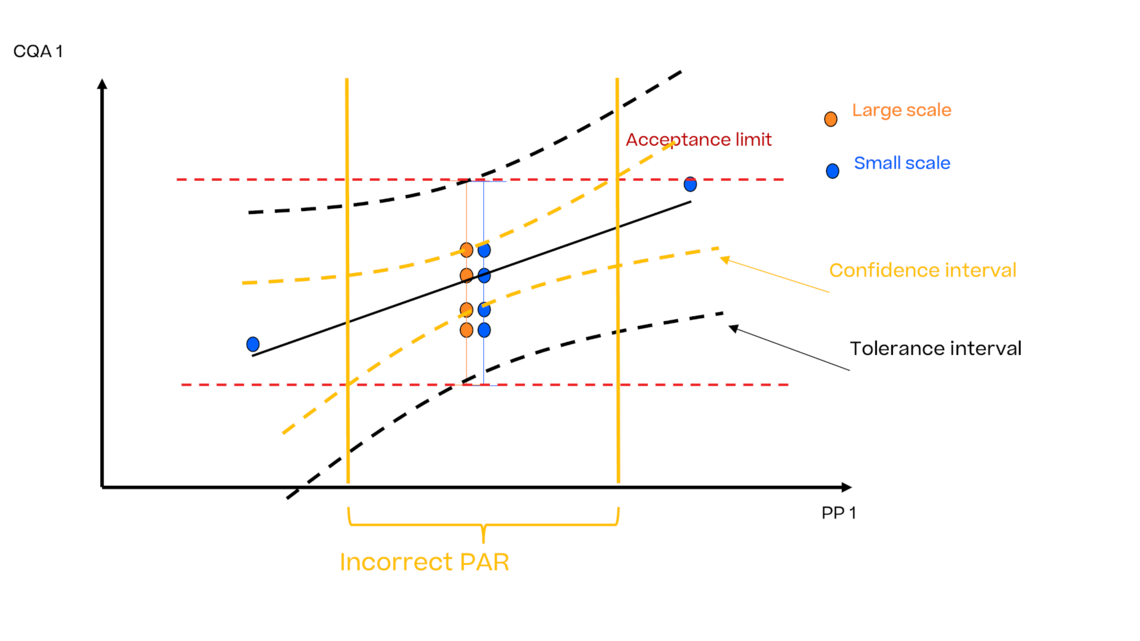
缺陷2

小规模模型没有代表性，即显示出比大规模更低的变异性。在这种情况下，形成的公差区间（黑色虚线）只代表小规模的变异性，而忽略了大规模模型的变异性。因此，如果不单独考虑小规模和大规模的平均值和方差是否具有可比性，控制策略对扩大生产的结果是无效的。

通过智能方法推导中间体的接受标准

如何使用可靠的统计方法来克服这些缺陷？

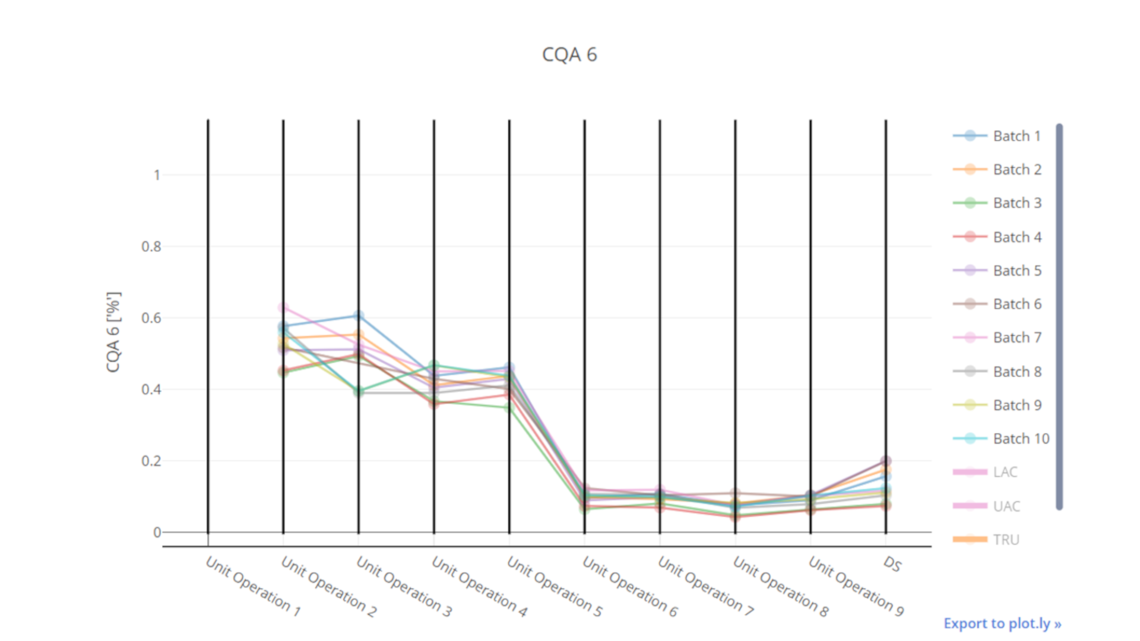
首先通过查看可以使用PAS-X Savvy生成的平行坐标图。在x轴上，我们看到了从第一次单元操作（UO）到原料药的工艺步骤序列。y轴显示了CQA的特定浓度，此处为杂质。每一行对应一个批次，该批次已通过整个UO链进行处理。该图在许多方面都能够提供帮助，例如证明杂质的主要清除发生在哪里，即在UO 6这种情况中。对于这张图我需要指出的是，一个特定单元操作的每个输出（也称为“池值”）都是下一个单元操作的输入（也称为“负载值”）。

考虑到这个想法，我们还可以用回归的方式表示数据，其中池值由负载值预测。首先，让我们关注这个过程的结束，即这个简单例子的UO3，其中存在原料药规范。我们可以利用回归模型来预测达到原料药规格的UO3的可接受负载值。由于UO 3的负载值等于UO 2的池值，我们已经找到了UO 2池值的可接受标准。这种非常简单的方法可以反复应用于UO 2和UO 1，以达到它们各自的接受限。有关这种方法的更多细节，请查看我们的出版物（Marschall等人，2022）。

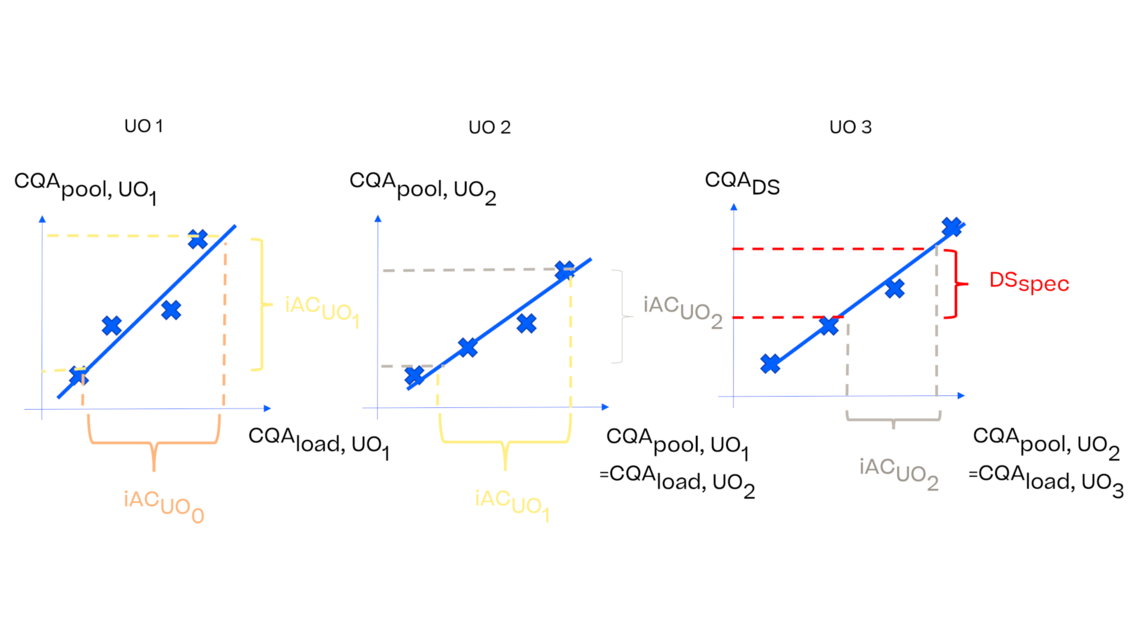
显然，统计数据有点复杂，因为我们需要考虑每个模型的模型不确定性。此外，我们还希望包括工艺参数对每个单元操作的（质量）输出的影响。这就是为什么需要使用过程集成模型（IPM）来以科学合理的方式解决这一问题。

总结

• 通常使用x-SD，例如3SD来设置接受标准的限值是存在缺陷的，为遵循合理的方法，只允许设定值条件来进行控制。
• 两个常见的缺陷之一是将不适当的统计区间，如置信区间与3SD得出的接受标准进行比较。另一个缺陷是没有考虑小规模和大规模的均值和方差的差异。
• 我们展示了一种合理的统计方法，不是从x-SD中得出的接受标准，而是在过程集成模型（IPM）框架内使用反向计算程序。使用这种方法，可以建立一种控制策略，真正确保在未来大部分生产运行的结果可以达到原料药规格。

了解更多